Abstrakt betrachtet setzt sich die Intralogistik aus Warenflüssen innerhalb eines Werkes zusammen. Diese Warenflüsse lassen sich auf einzelne Transportaufträge herunterbrechen. Ein Beispiel hierfür ist der Transportauftrag zum Auslagern von Bauteilen auf einer Palette aus dem Palettenlager, welche für die Weiterverarbeitung an einer Maschine transportiert wird. Je nach Größe des Werkes fallen solche Prozesse täglich hunderte, tausende Male oder sogar noch öfter an.
Komplexität von intralogistischen Prozessen
Mit wachsender Anzahl an Transportaufträgen und zusätzlichen Bedingungen, wie Fälligkeiten, oder der Kombinationsmöglichkeit von Transportaufträgen wird es immer wichtiger die Prozesse und Wege zwischen den Aufträgen zu optimieren. Die Bildung der Reihenfolge, in der die Transportaufträge abgehandelt werden, kann simpel erfolgen, zum Beispiel wenn die Transporte auf Sicht abgearbeitet werden. Wenn in die Abarbeitungsreihenfolge der Transportaufträge hingegen zusätzliche Informationen über die anderen Transportaufträge einfließen, wird die optimale Zuweisungsreihenfolge der Transportaufträge mit wachsender Anzahl an Transportaufträgen sehr schnell komplex. Zusätzlich können die Transporte von unterschiedlichen Fahrzeugen im System abgearbeitet werden, was ebenfalls die Komplexität anhebt.
Mathematischer Hintergrund – Das Vehicle Routing Problem
Das Problem ist in der Mathematik als Vehicle Routing Problem (VRP) bekannt. Das VRP ist eine Erweiterung des multiple Traveling Sales Man Problem (mTSP), welches neben mehreren Instanzen, die Aufträge parallel erledigen können, auch Transportkapazitätsrestriktionen betrachtet.
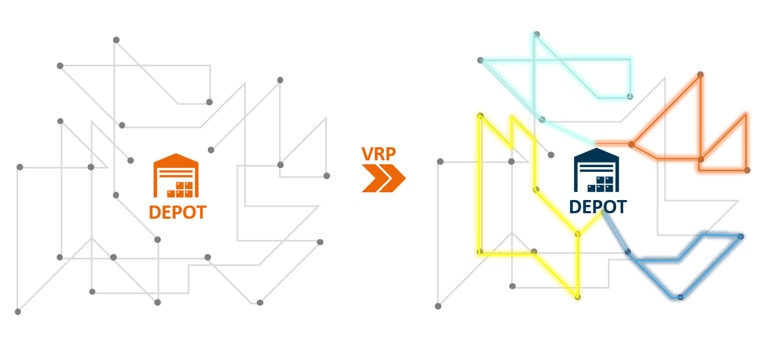
Bei dem normalen VRP wird von einem zentralen Depot als Start- und Endpunkt jeder Tour ausgegangen, was in der Intralogistik allerdings nicht vorausgesetzt werden kann. Es müssen dezentralisierte PickUp (Aufnahmepunkte) und Deliverys (Abgabepunkte) betrachtet werden. Zusätzlich gibt es durch Fälligkeitszeitpunkte Einschränkungen auf der Zeitschiene. Die für die Intralogistik typische Problemvariante wird als Erweiterung zum normalen VRP als Vehicle Routing Problem with Pickup and Delivery and with Time Windows (VRPPDTW) bezeichnet.
Problemlösung und Annäherung
Das VRP ist ein NP-schweres Problem. Sollte das Problem daher exakt gelöst werden, so wächst mit der Größe des Inputs die Laufzeit stärker als eine Expotentialfunktion. Wenn beispielsweise das exakte Lösen des Problems bei 10 Transportaufträgen ungefähr 5 Sekunden dauert, würde das exakte Lösen von 100 Aufträgen 3.86*1031 Jahre dauern. Deshalb wird bei solchen Problemen nicht die exakte Lösung berechnet, sondern es wird die beste Lösung, die innerhalb eines festen Zeitraums gefunden werden kann, ausgewählt.
Vorgehensweise zur Berechnung
Dieser Prozess kann in zwei Schritte gegliedert werden, das Finden einer initialen Lösung und die Optimierung dieser Lösung. Um die unterschiedlichen Lösungen bewerten zu können, muss eine Funktion zur Verfügung gestellt werden, die die unterschiedlichen Lösungen nach Güte vergleichbar macht. Die sogenannte Bewertungsfunktion vergleicht und bewertet Größen wie zurückgelegte Gesamtwegstrecke und Fälligkeitsverletzungen. Beispielsweise wird abgewogen, bis zu welchem Maß eine Fälligkeitsverletzung akzeptiert wird, wenn es zu einer genügend starken Reduktion des Gesamtfahrwegs führt.
Als erster Schritt wird eine valide Lösung ermittelt, welche die zuvor festgelegten Kriterien erfüllt. Mit dieser ersten Lösung wird dann versucht, weitere Verbesserungen zu finden. Die Algorithmen, die dazu verwendet werden, heißen Meta-Heuristiken und Beispiele dafür sind der TABU-Search oder der HillClimb Algorithmus. Um die Verbesserungen zu finden, wird die vorhandene Lösung leicht angepasst, zum Beispiel werden Aktionen getauscht oder es wird versucht, Aktionen an anderen Stellen einzufügen. Die Modifikation, die zu den größten Verbesserungen führt, wird übernommen. Je nach ausgewähltem Algorithmus werden mehr oder weniger Möglichkeiten ausprobiert und dann die bestmögliche Lösung ausgewählt. Meta-Heuristiken wie der TABU-Search können auch mit Voraussicht aus lokalen Extremwerten heraus manövrieren, um ein globales Minimum oder Maximum zu erreichen.
Fazit
Insgesamt kann mit dieser Methodik zwar nicht gewährleistet werden, dass immer die optimale Lösung des Problems gefunden wird, aber viel wichtiger für die praktische Anwendung kann diese Lösung innerhalb von vorgegebenen Zeitfenstern gefunden werden. Hierbei ist immer die Prämisse: Umso schneller der Algorithmus arbeitet umso mehr Optimierungspotential wird ausgereizt.

Autor – Jonathan Hohm
Data Analyst & KI Entwickler
Im Rahmen seiner Tätigkeit bei Flexus optimiert er mit den passenden Optimierungsalgorithmen die Intralogistik unserer Kunden. Dies findet vor allem Anwendung bei der Optimierung von Staplern, Routenzuglogiken und der effizienten Steuerung von AGVs.

